[轉錄]16 Lectures on Basic Computer Concepts---C (Chinese) 計算機概論十六講---Ｃ

<h2>本篇文章原始來源:http://libai.math.ncu.edu.tw/bcc16/C/C/b10-1.shtml



使用函式做數學計算的範例 </h2>
<h3>牛頓求根迭代法</h3>

若 <i>f</i>(<i>x</i>) 是一次可微且導函數連續的函數，則牛頓求根法的迭代公式是

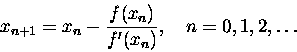
其中 <i>x</i>₀ 是初始猜想值 (initial guess)。牛頓求根法產生一個數列 <i>x</i>₀, <i>x</i>₁, <i>x</i>₂, ... 這個數列不一定收斂，即使收斂也不一定收斂到 <i>f</i>(<i>x</i>) 的一個根。但是通常如果 <i>x</i>₀ 很靠近所求的根，則 <i>n</i> 不必超過 10 就足夠使得 <i>f</i>(<i>x</i>_<i>n</i>) 幾乎是 0。

 

以下這個程式，將 和它的導函數 定義成兩個 C 語言函式 <tt>f()</tt> 和 <tt>df()</tt>，然後用牛頓法求一個近似根。程式中的所有浮點數都用雙精度，取 <i>x</i>₀ = 0.5，讓電腦迭代 10 次之後停下來，輸出每次的 <i>x</i>_<i>n</i>。這個程式需要數學函式。

---

#include <stdio.h>
#include <math.h>
/* 示範牛頓求根迭代法  (newton-iteration.c) */
#define STEP 10
double f(double);
double df(double);
main() {
int n;
double x;
x = 0.5;
for (n=0; n < STEP; ++n) {
x = x - f(x)/df(x);
printf("x_%-2d = %17.14f\n", n+1, x);
}
}
double f(double x) {
return sqrt(x) - cos(x);
}
double df(double x) {
return 1/(2*sqrt(x)) + sin(x);
}

---

我必須提醒讀者，以上程式在技巧上和數學問題的處理上，都還有改進之處。例如我們沒有考慮發生零分母的可能。它只是一個範例而已。注意在 <tt>f()</tt> 和 <tt>df()</tt> 中，使用 <tt>return</tt> 的技巧。執行這個程式，可以明顯地看到數字收斂的效果，其實在 <i>x</i>₄ 之後，迭代數值的前 14 位有效數字就已經不變了，因此可以說前 14 位有效數字「已經收斂」了。

 

<h3>梯形數值積分法</h3>

若 <i>f</i>(<i>x</i>) 在 [<i>a</i>,<i>b</i>] 中連續，則可積。 梯形數值積分法 (trapezoidal rule) 是求定積分之近似值的一種方法，其公式如下

其中 <i>n</i> 表示將 [<i>a</i>,<i>b</i>] 等分成 <i>n</i> 段，令

而且 <i>x</i>₀ = <i>a</i>、 <i>x</i>_<i>n</i> = <i>b</i>，一般而言 <i>x</i>_<i>k</i> = <i>a</i> + <i>k h</i>。

 

以下這個程式，示範以梯形數值積分法求

的定積分近似值。此程式將被積分函數定義成 C 函式 <tt>f()</tt>，所有浮點數用雙精度計算，並依序用 <i>n</i>=2, 4, 8, 16,..., 2¹⁶ 算梯形積分值，輸出對應每個 <i>n</i> 的定積分近似值。這個程式需要呼叫數學函式。

---

#include <stdio.h>
#include <math.h>
/* 示範梯形數值積分法  (trapeziodal.c) */
#define STEP 16
double f(double);
main() {
int n, k, i;
double h, T, a, b, x;
T = 0;
a = 0;
b = 1;
for (n=1, i=0; i < STEP; ++i) {
n = 2*n;
h = (b-a)/n;
x = a;
T = f(x)/2;
for (k=1; k<n ; ++k) {
x = x + h;
T = T + f(x);
}
T = T + f(b)/2;
T = h*T;
printf("T_%-5d = %17.14f.\n", n, T);
}
}
double f(double x) {
return sqrt(1+x*x*x);
}
</pre>

我必須提醒讀者，以上程式在技巧上和數學問題的處理上，都還有改進之處。此處只是示範而已。 0鶡瘜o個程式，可以清楚地看到梯形積分數值的收斂情況，也就是說，隨著 <i>n</i> 的增加，<i>T</i><i>n</i> 就有越來越多的有效數字是不變的。而這些不再隨 <i>n</i> 而改變的有效數字，就是「已經收斂」的數字，它們是可靠的答案。例如，我們應該可以相信 <i>T</i>65536 已經準確到小數點下第 9 位。
 
<h3>Collatz 猜想</h3>
任取一個正整數 <i>p</i>，令 <i>x</i>0 = <i>p</i> 且定義 Collatz 數列如下： 


 
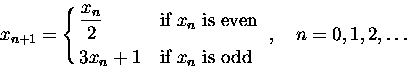
所謂的 Collatz 猜想，就是說數列 <i>x</i><i>n</i> 必定會出現 1。根據 Collatz 數列的定義，一旦出現 1，接下去就是 1,4,2,1,4,2,... 這樣的循環。到寫教材的時候為止，Collatz 猜想還是個未解決的問題：亦即，尚未證明它對，也沒找到它錯的反例。
 
以下這個程式，為 Collatz 猜想做一些實驗。我們依序取 <i>p</i> = 1,2,3,...,1000，對每一個 <i>p</i>，定義 <i>t</i>(<i>p</i>) 是使得 <i>x</i><i>t</i>(<i>p</i>) = 1 *熙怳p整數。例如若 <i>p</i>=1 則因為 <i>x</i>0=1 所以 <i>t</i>(1) = 0。若 <i>p</i>=2 則因為 <i>x</i>0=2 然後 <i>x</i>1=1 所以 <i>t</i>(2) = 1。若 <i>p</i>=3 則因為 
<i>x</i>0=3 <i>x</i>1=10 <i>x</i>2=5 <i>x</i>3=16 <i>x</i>4=8 <i>x</i>5=4 <i>x</i>6=2 <i>x</i>7=1 
所以 <i>t</i>(3) = 7。依此類推。以下這個程式，定義一個函式 <tt>collatz()</tt>，輸入正整數 <i>p</i>，輸出整數 <i>t</i>(<i>p</i>)，輸出每一對的 <i>p</i> 和 <i>t</i>(<i>p</i>)，並輸出 <i>t</i>(<i>p</i>) 最大的情況。 

#include <stdio.h>
/* 示範 Collatz 猜想的實驗 (collatz.c) */
#define SIZE 1000
int collatz(int);
main () {
int p, tp, maxp, maxtp;
maxp = maxtp = 0;
for (p=1; p<=SIZE; ++p) {
tp = collatz(p);
printf("%4d: %4d\n", p, tp);
if (tp > maxtp) {
maxp = p;
maxtp = tp;
}
}
printf("for p=0..%d, max t(%d) = %d\n", SIZE, maxp, maxtp);
}
int collatz(int p) {
int x=p, n=0;
while (x != 1) {
if (x%2 == 1)
x = 3*x + 1;
else
x = x/2;
++n;
}
return n;
}


以上程式仍然是在技巧上還有改進之處。此處的主要目的，是示範如何利用計算機從事數學實驗。從這一千對的 <i>p</i> 和 <i>t</i>(<i>p</i>) 看來，Collatz 猜想都是正確的，事實上讀者可以做更多的測試，到目前為止沒有找到 Collatz 猜想的反例。
 
習題



    
用牛頓求根法迭代 10 次，計算 <i>e</i>-<i>x</i> = sin <i>x</i> 最靠近 0 的近似根。說明這個近似根有幾位準確的有效數字。 
    
用 216 個等分點的梯形數值積分法，估計以下定積分 

    
 
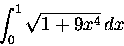
    說明這個近似值有幾位準確的有效數字。 
    
令 <i>p</i>=5,6,7,...,15, 列出當 <i>x</i>0 = <i>p</i> 所產生的 Collatz 數列，直到第一次出現 1 為止。 

 
[ 前一節 ]‧[ 後一節 ]‧[ 回目錄 ]



注意：此處所有文件均為原著，個別的版權宣告日後會一一公布，整體版面設計亦尚未完成。但仍請勿抄襲文字與圖片，以免觸犯著作權法。 
Created: Feb 24, 2001

Last Revised: Feb 25, 2001

© Copyright 2001 Wei-Chang Shann 單維彰





    
Back to the home page of Wei-Chang Shann. 
    
Connect to the home page of Department of Mathematics, National Central University, Tai